A háromszög és a szögfüggvények
Háromszög:
Három pont által meghatározott három szakasz háromszöget alkot, illetve határol.

A szögeket - általában is, nem csak a háromszögön belül - a görög ABC kisbetűivel jelöljük. A háromszög egyes oldalait a vele szemben lévő szögnek megfelelően, a latin ABC kisbetűivel jelöljük.
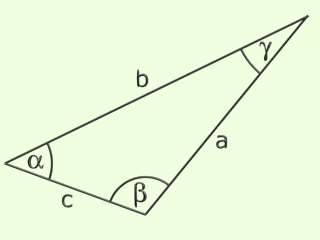
A háromszög szögeinek összege 180 fok.
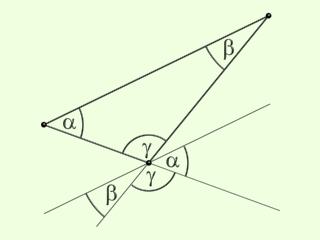
A háromszög valamely csúcsába futó szakaszokat egészítsük ki a csúcson túl futó félegyenesekké. A csúcson át húzzunk egyenest, amely a csúcsal szembeni oldallal párhuzamos. Így a csúcson három, az eredeti háromszögön kívül lévő szöget kaptunk, amelyekre a következő állítások igazak:
- az egyik szög két szára a háromszög egyik szögének két szárával azonos egyenesen fekszik, ezért azzal egyenlő
- a másik két szög két szára a háromszög egy-egy szögének egyik szárával párhuzamos, a másikkal közös egyenesen fekszik, ezért azzal egyenlő.
A kapott három szög az egyenes egyik pontjától a másikig tartó körívet ad ki, vagyis 180 fokos, ezért a háromszög szögeinek összege is 180 fok.
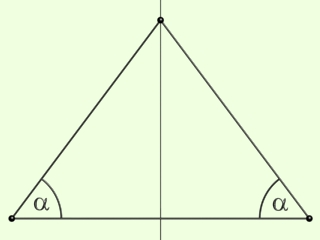
Az egyenlő szárú háromszög alapján fekvő két szöge egyenlő.
A háromszög csúcsából állítsunk merőlegest a háromszög alapjára. Erre a merőlegesre tükrözve az egyik alapon fekvő szög csúcsát és szárait, a másik alapon fekvő szöget kapjuk meg, tehát nagyságuk egyenlő.
Thales-tétel:
Ha egy háromszög alapja egy kör átmérőjét képezi, az alapjával szemben lévő csúcsa pedig ugyanazon körön fekszik, akkor az alapjával szembeni szöge derékszög.
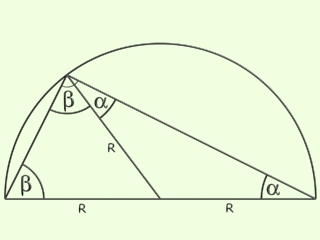
Húzzunk egyenest a kör középpontjából a háromszög alappal szembeni csúcsához. Ezzel két egyenlő szárú háromszöget kapunk, amelyek alapon fekvő szögei az eredeti háromszög szögeit adják ki, ezért összegük 180 fok.
a+a+b+b = 180 fok
2*a + 2*b = 180 fok
2*(a+b) = 180 fok
a+b = 90 fok
Derékszögű háromszög:
Az olyan háromszöget, melynek egyik szöge derékszög, derékszögű háromszögnek nevezzük. A háromszög azon oldalait, amelyek a derékszög szárait alkotják, befogónak, a harmadik - leghosszabb - oldalát átfogónak nevezzük.
A derékszögű háromszögben általában a kisebbik befogót jelöljük "a"-val, a nagyobbikat "b"-vel és az átfogót "c"-vel.

Szögfüggvények:
A szögfüggvények az egységnyi átmérőjű derékszögű háromszög oldalainak és szögeinek összefüggéseit írják le.
Vegyünk egy ilyen háromszöget, és tekintsük az egyik, nem derékszögű szögét. Könnyen belátható, hogy minél kisebb ez a szög, a szöggel szembeni befogó is annál kisebb, a szög melletti befogó pedig annál nagyobb; minél nagyobb ez a szög, a szöggel szembeni befogó is annál nagyobb, a szög melletti befogó annál kisebb.
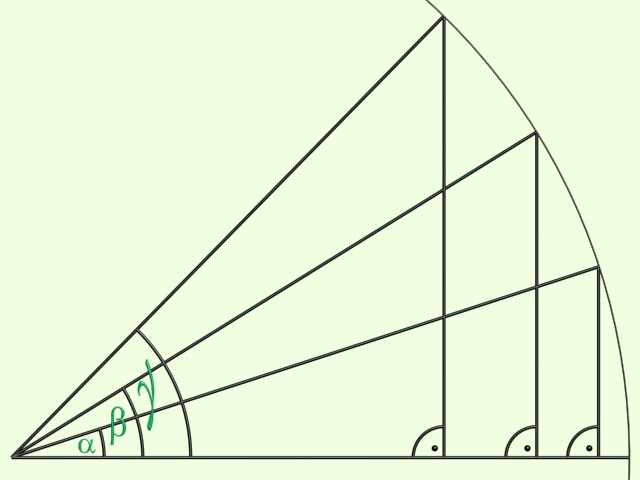
A szöggel szembeni befogó és az átfogó arányát (befogó/átfogó) az adott szög sinusának nevezzük.
sin(a) = a/c
A szög melletti befogó és az átfogó aránya az adott szög cosinusa.
cos(a) = b/c
E két szögfüggvény értékei bármely nagyságú átfogó esetén azonosak, adott szögek mellett.
A szöggel szembeni befogó és a szög melletti befogó aránya a szög tangense, ez egyenlő a szög sinusának és cosinusának arányával.
tg(a) = a/b
tg(a) = sin(a)/cos(a)
A szög melletti befogó és a szöggel szembeni befogó aránya a szög cotangense, ami a szög cosinusának és sinusának arányával egyenlő.
ctg(a) = b/a
ctg(a) = cos(a)/sin(a)
Mivel az egyik szög mellett fekvő befogó a másik szöggel szemben fekszik illetve az egyik szög melletti befogó a másik szöggel szembeni befogó, ezért az egyik szög sinusa egyúttal a másik szö cosinusa is. Mivel pedig e két szög a derékszögű háromszögben 90 fokra kell, hogy kiegészítsék egymást (lévén, a háromszög szögeinek összege 180 fok), ezért:
sin(a) = cos(90-a)
cos(a) = sin(90-a)
Az eddig elmondottak a 0° és 90°közötti szögekre vonatkoznak. A szögekkel végzett matematikai műveletek miatt (összeadás, kivonás) azonban később szükségünk lesz a 90 fokosnál nagyobb, vagy éppen 0 fokosnál kisebb szögek sinus és cosinus függvények értékeire is, ezért ezeket is értelmeznünk kell.
Először állapítsuk meg, hogy mit értünk negatív szögön. Ha egy egyenesre szöget állítunk, akkor az egyenestől a szög másik szárához, az óramutató járásával ELLENKEZŐ irányban elvezető körív által alkotott szöget pozítívnak tekintjük, az óramutató járásával MEGEGYEZŐ irányban elvezetőt pedig negatívnak.
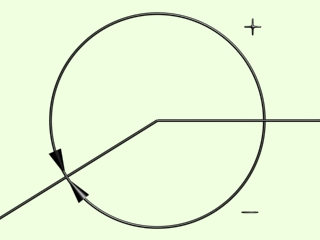
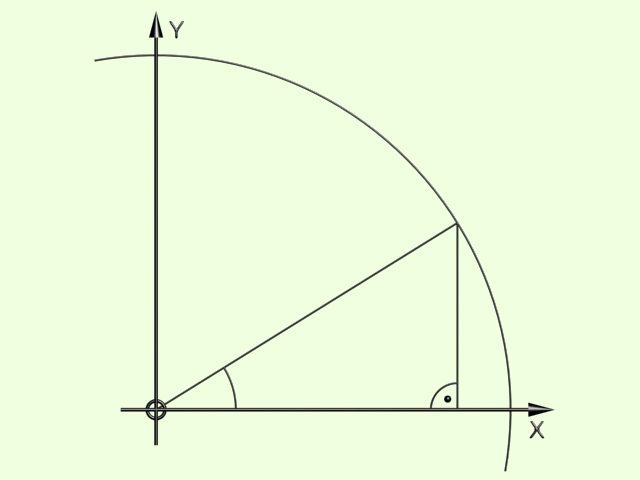
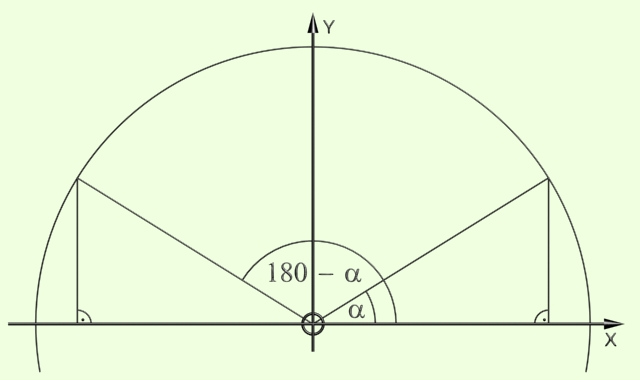
Az ábrára nézve belátható, hogy:
sin( 180 - a ) = sin( a )
cos( 180 - a ) = - cos( a )
Ha szögünk 180 és 270 fok közé esik, akkor egy 0 és 90 fok közé eső szögből származtatható, oly módon, vagy hozzáadunk 180 fokot. Ekkor mind a sinus, mind a cosinus érték negatív lesz.
sin( 180 + a ) = - sin( a )
cos( 180 + a ) = - cos( a )
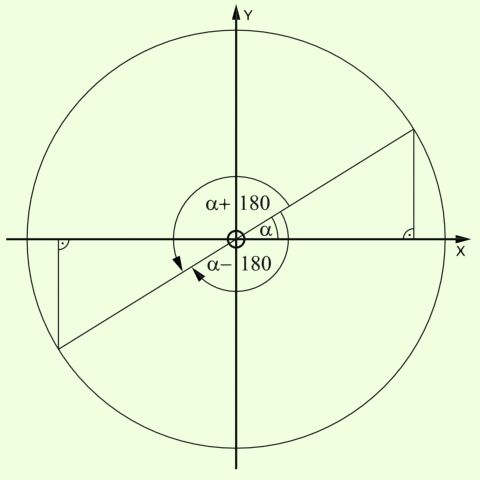
Az ábrából látható, hogy ugyanezeket a sinus és cosinus értékeket kapjuk meg akkor is, ha az a értékéhz nem hozzáaadunk 180 fokot, hanem levonjuk belőle, íly módon -90 és -180 fok közötti szögre téve szert.
sin( a - 180 ) = - sin( a )
cos( a - 180 ) = - cos( a )
Végül, ha szögünk 270 és 360 fok közé (vagy -90 és 0 fok közé) esik, akkor sinusa negatív, cosinusa pozitív értékü lesz.
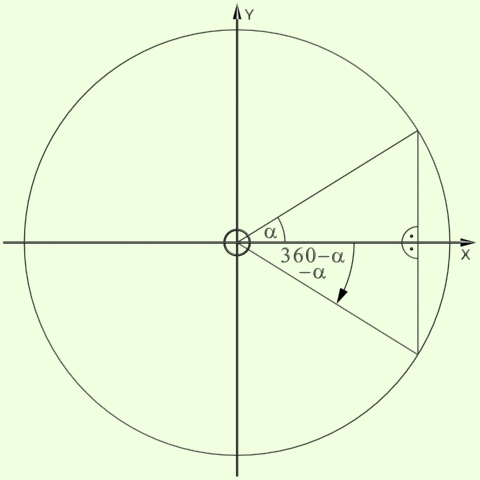
sin( 0 - a ) = - sin( a )
cos( 0 - a ) = cos( a )
sin( 360 - a ) = - sin( a )
cos( 360 - a ) = cos( a )
(A sinus és cosinus függvény szempontjából tehát mindegy, hogy paraméterének a vizsgált szöget magát vesszük-e, vagy az azt 360 fokra kiegészítő szöget. 330 fok sinusa és kosinusa ugyanaz, mint -30 foké, -115 foké ugyanaz mint 245 foké, és így tovább.)
A sinus függvény értékét adott X szögek esetében eleinte a legegyszerűbb módon, méréssel határozták meg: minél nagyobb méretű háromszögeket rajzoltak, és lemérték ezek oldalhosszúságait. Később rájöttek, hogy léteznek olyan matematikai sorozatok, amelyek annál jobban közelítik a sinus függvény értékét, minél több tagot tartalmaznak. Ezek egyike (X értéke itt radiánban értendő):
$$ { \sin{ x } = x - \left( \frac{x^3}{3!} \right) + \left( \frac{x^5}{5!} \right) - \left( \frac{x^7}{7!} \right) + \left( \frac{x^9}{9!} \right) \text{...} } $$Általános formában leírva, a sorozat n. tagja (beleértve az n=0 esetet is):
$$ { \left( -1 \right)^n * \left( \frac{ x^\left( 2n+1 \right) } { \left( 2n+1 \right)! } \right) } $$azaz:
$$ { \sin{x} = \sum_{n=0}^{\infty} \left( \left( -1 \right)^n * \left( \frac{ x^\left( 2n+1 \right) } { \left( 2n+1 \right)! } \right) \right) } $$A Cos( X ) értékét Sin( X ) -ből már egyszerűen meghatározhatjuk, de ennek is létezik végtelen soroazata:
$$ { \cos{ x } = 1 - \left( \frac{x^2}{2!} \right) + \left( \frac{x^4}{4!} \right) - \left( \frac{x^6}{6!} \right) + \left( \frac{x^8}{8!} \right) \text{...} } $$Általános formában leírva, a sorozat n. tagja (beleértve az n=0 esetet is):
$$ { \left( -1 \right)^n * \left( \frac{ x^\left( 2n \right) } { \left( 2n \right)! } \right) } $$azaz:
$$ { \cos{x} = \sum_{n=0}^{\infty} \left( \left( -1 \right)^n * \left( \frac{ x^\left( 2n \right) } { \left( 2n \right)! } \right) \right) } $$